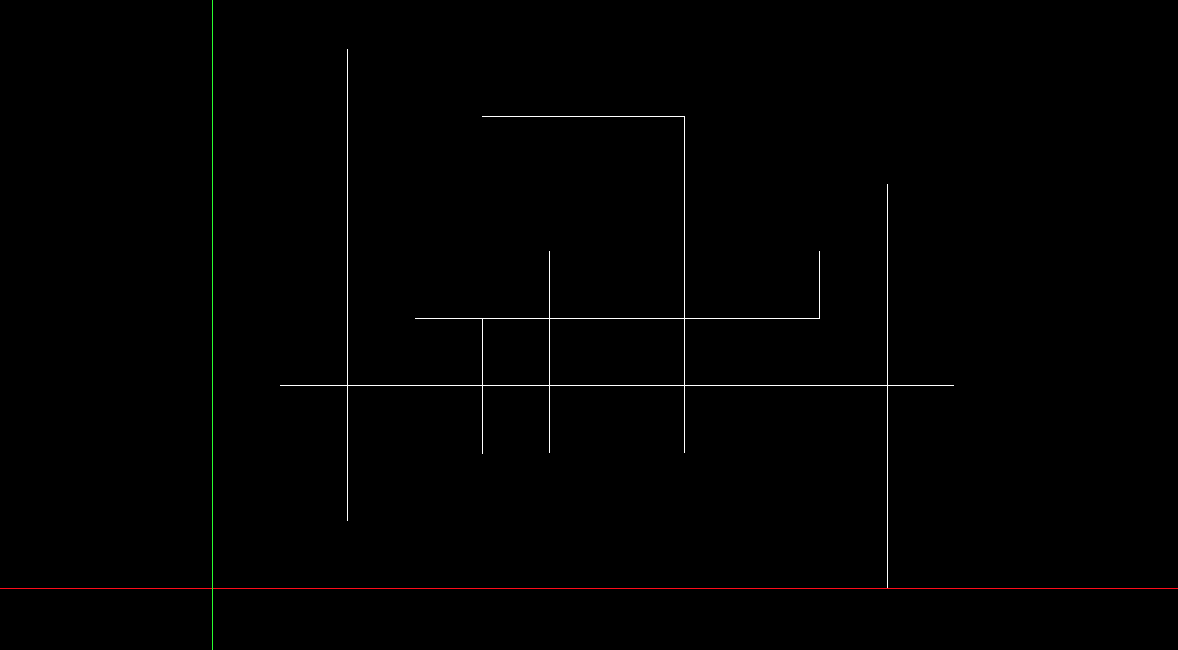
Table of contents

# Problem

http://judge.u-aizu.ac.jp/onlinejudge/description.jsp?id=CGL_6_A

Report the number of intersections of given vertical or horizontal segments.

# Explanation

Segment intersections | Line sweep algorithm

# Time complexity

O(N \log N)

# Solution

// C++ 14
#include <iostream>
#include <string>
#include <vector>
#include <list>
#include <algorithm>
#include <queue>
#include <stack>
#include <set>
#include <map>
#include <unordered_map>
#include <math.h>

#define ll long long
#define Int int
#define loop(x, start, end) for(Int x = start; x < end; x++)
#define loopdown(x, start, end) for(int x = start; x > end; x--)
#define rep(n) for(int x = 0; x < n; x++)
#define span(a,x,y) a.begin()+x,a.begin()+y
#define span_all(a) a.begin(),a.end()
#define len(x) (x.size())
#define last(x) (*(x.end()-1))

using namespace std;

#define EPS 0.0000000001
#define fequals(a,b) (fabs((a) - (b)) < EPS)

class Vector2 {
public:
  double x, y;
  
  Vector2(double x = 0, double y = 0): x(x), y(y) {}
  
  Vector2 operator + (const Vector2 v) const { return Vector2(x + v.x, y + v.y); }
  Vector2 operator - (const Vector2 v) const { return Vector2(x - v.x, y - v.y); }
  Vector2 operator * (const double k) const { return Vector2(x * k, y * k); }
  Vector2 operator / (const double k) const { return Vector2(x / k, y / k); }
  
  double length() { return sqrt(norm()); }
  double norm() { return x * x + y * y; }
  double dot (Vector2 const v) { return x * v.x + y * v.y; }
  double cross (Vector2 const v) { return x * v.y - y * v.x; }
  
  bool parallel(Vector2 &other) {
    return fequals(0, cross(other));
  }
  
  bool orthogonal(Vector2 &other) {
    return fequals(0, dot(other));
  }
  
  bool operator < (const Vector2 &v) {
    return x != v.x ? x < v.x : y < v.y;
  }
  
  bool operator == (const Vector2 &v) {
    return fabs(x - v.x) < EPS && fabs(y - v.y) < EPS;
  }
};

ostream & operator << (ostream & out, Vector2 const & v) { 
  out<< "Vector2(" << v.x << ", " << v.y << ')';
  return out;
}

istream & operator >> (istream & in, Vector2 & v) { 
  double x, y;
  in >> x;
  in >> y;
  v.x = x;
  v.y = y;
  return in;
}

Int N;
vector<Point> points;
Point p1, p2;
set<Int> BT;

Int line_sweep() {
  Int count = 0;
  sort(span_all(points));
  
  for (auto p: points) {
    switch (p.type) {
      case DOWN:
        BT.insert(p.coord.x);
        break;
      case LEFT:
        count += distance(
          lower_bound(span_all(BT), p.coord.x),
          upper_bound(span_all(BT), p.coord.x + p.length)
        );
        break;
      case UP:
        BT.erase(p.coord.x);
        break;
      case RIGHT:
        // do nothing
        break;
    }
  }
  return count;
}

void solve() {
  cout << line_sweep() << endl;
}

void input() {
  cin >> N;
  loop(n,0,N) {
    cin >> p1.coord >> p2.coord;
    if (p1.coord.y == p2.coord.y) {
      if (p1.coord.x < p2.coord.x) p1.type = LEFT,p2.type = RIGHT;
      else p1.type = RIGHT,p2.type = LEFT;
      p1.length = p2.length = fabs(p1.coord.x - p2.coord.x);
    } else {
      if (p1.coord.y < p2.coord.y) p1.type = DOWN,p2.type = UP;
      else p1.type = UP,p2.type = DOWN;
      p1.length = p2.length = fabs(p1.coord.y - p2.coord.y);
    }
    points.push_back(p1), points.push_back(p2);
  }
}

int main() {
  input();
  solve();
}

CGL_6_A | Segment intersections (Manhattan Geometry)

# Problem

# Explanation

# Time complexity

# Solution

Comments