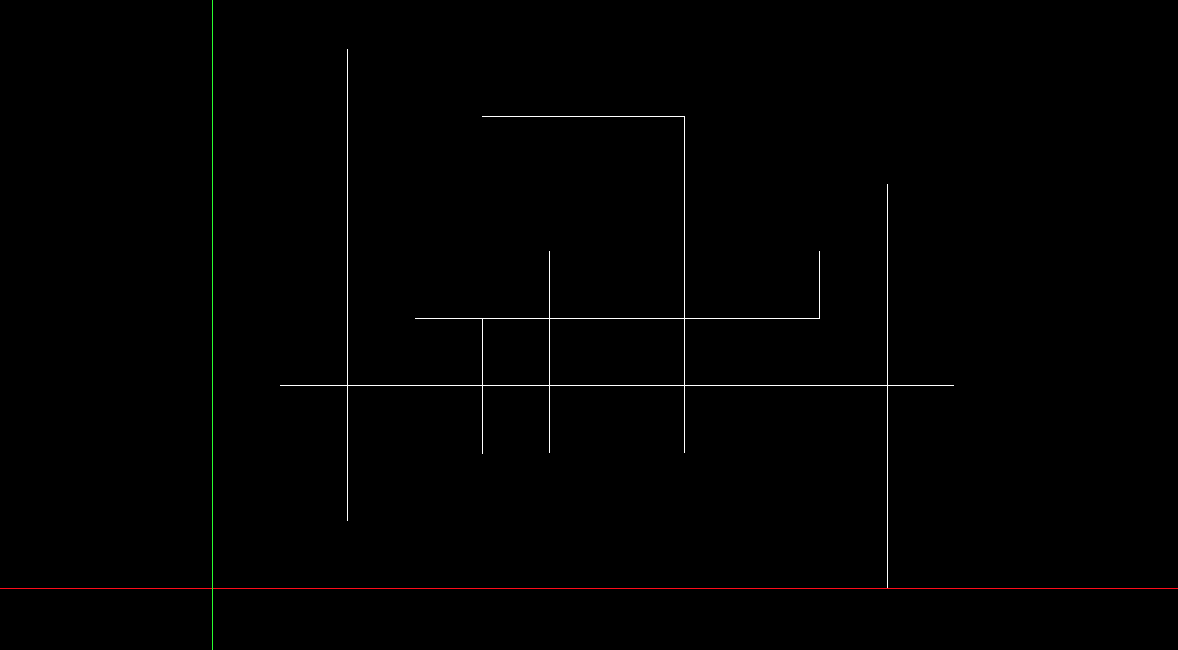
Table of contents

# Usage

Given vertical or horizontal segments, report the number of intersections of them.

# Algorithm

Add following properties to each point.
- type: bottom or top of vertical segments (DOWN, UP). left or right of horizontal segments (LEFT, RIGHT).
- length: the length of segment which the point belongs to.
Sort all the points according to the following:
- y ascending
- if y is a tie, type ascending(DOWN -> LEFT -> UP -> RIGHT)
- if type is a tie, x ascending
Initliaze counter with 0
Execute followings for each point
- type is UP) Insert x coordinate to Binary Tree BT
- type is LEFT) Add the number of elements to counter which is within x coordinate and x + length.
- type is DOWN) Erase x from BT

# Time Complexity

$O(N \log N)$ for sorting points.

After that, insertion, deletion and search of set are $O(\log N)$ .
Repeat it $N$ times. $N$ stands for the number of points.

$O(N \log N)$

# Code

// C++ 14
#include <iostream>
#include <string>
#include <vector>
#include <list>
#include <algorithm>
#include <queue>
#include <stack>
#include <set>
#include <map>
#include <unordered_map>
#include <math.h>

#define ll long long
#define Int int
#define loop(x, start, end) for(Int x = start; x < end; x++)
#define loopdown(x, start, end) for(int x = start; x > end; x--)
#define rep(n) for(int x = 0; x < n; x++)
#define span(a,x,y) a.begin()+x,a.begin()+y
#define span_all(a) a.begin(),a.end()
#define len(x) (x.size())
#define last(x) (*(x.end()-1))

using namespace std;

#define EPS 0.0000000001
#define fequals(a,b) (fabs((a) - (b)) < EPS)

class Vector2 {
public:
  double x, y;
  
  Vector2(double x = 0, double y = 0): x(x), y(y) {}
  
  Vector2 operator + (const Vector2 v) const { return Vector2(x + v.x, y + v.y); }
  Vector2 operator - (const Vector2 v) const { return Vector2(x - v.x, y - v.y); }
  Vector2 operator * (const double k) const { return Vector2(x * k, y * k); }
  Vector2 operator / (const double k) const { return Vector2(x / k, y / k); }
  
  double length() { return sqrt(norm()); }
  double norm() { return x * x + y * y; }
  double dot (Vector2 const v) { return x * v.x + y * v.y; }
  double cross (Vector2 const v) { return x * v.y - y * v.x; }
  
  bool parallel(Vector2 &other) {
    return fequals(0, cross(other));
  }
  
  bool orthogonal(Vector2 &other) {
    return fequals(0, dot(other));
  }
  
  bool operator < (const Vector2 &v) {
    return x != v.x ? x < v.x : y < v.y;
  }
  
  bool operator == (const Vector2 &v) {
    return fabs(x - v.x) < EPS && fabs(y - v.y) < EPS;
  }
};

ostream & operator << (ostream & out, Vector2 const & v) { 
  out<< "Vector2(" << v.x << ", " << v.y << ')';
  return out;
}

istream & operator >> (istream & in, Vector2 & v) { 
  double x, y;
  in >> x;
  in >> y;
  v.x = x;
  v.y = y;
  return in;
}

enum PointType {
  DOWN, LEFT, UP, RIGHT // The order matters.
};

class Point {
public:
  Vector2 coord;
  PointType type;
  Int length;
  
  bool operator < (const Point &p) {
    // if y is a tie, use type.
    return (p.coord.y == coord.y && type != p.type)
      ? type < p.type
      : coord < p.coord;
  }
  
  bool operator == (const Point &p) {
    return coord == p.coord && type == p.type;
  }
};

Int line_sweep() {
  set<Int> BT;
  Int count = 0;
  sort(span_all(points));
  
  for (auto p: points) {
    switch (p.type) {
      case DOWN:
        BT.insert(p.coord.x);
        break;
      case LEFT:
        count += distance(
          lower_bound(span_all(BT), p.coord.x),
          upper_bound(span_all(BT), p.coord.x + p.length)
        );
        break;
      case UP:
        BT.erase(p.coord.x);
        break;
      case RIGHT:
        // do nothing
        break;
    }
  }
  return count;
}

Segment intersections | Line sweep algorithm

# Usage

# Algorithm

# Time Complexity

# Code

Comments